Rumus Bangun Ruang Lengkap - Didalam matematika yang dimaksud dengan bangun ruang ini biasanya suatu bangun yang memiliki isi atau bentuk 3 dimensi (secara grafik : x, y, z). Atau secara sederhana anda bisa membayangkan sewaktu anda didalam ruangan. Anda dan semua benda-benda yang ada diruangan tersebut termasuk sebagai isi dari bangun ruang (ruangan tersebut). Jika suatu bangun itu tidak memilki isi atau hanya berbentuk 2 dimesi maka disebut sebagaibangun datar. Yang pasti pada suatu bangun ruang selalu ada volume atau isi. Semua benda yang ada di dunia ini sebenarnya sebagian besar berbentuk bangun ruang. Karena benda-benda tersebut kebanyakan mempunyai bentuk 3 dimensi. Hanya saja pada benda tersebut ada juga bagian yang disebut bangun datar yaitu pada bagian permukaannya saja.
Setiap bangun ruang memiliki rumus perhitungan yang berbeda-beda pula tergantung dari bentuknya masing-masing. Secara umum bangun ruang matematika digolongkan menjadi kubus, balok, bola, tabung, limas, kerucut dan prisma. Jika anda seorang ahli matematika biasanya anda sudah paham betul dengan rumus-rumus tersebut. Pada artikel ini saya coba tulis mengenai rumus bangun ruang dan gambarnya.
 |
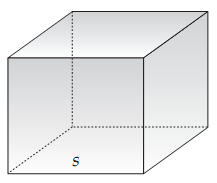
| Bangun Ruang Kubus |
Ketetuan pada bangun ruang kubus :
a. Terdapat 6 (enam) buah sisi yang berbentuk persegi dengan masing-masing luasnya sama
b. Terdapat 12 (dua belas) rusuk dengan panjang yang sama
c. Semua sudut bernilai 90 derajat atau siku-siku
d. Rumus Volume Kubus = rusuk x rusuk x rusuk (rusuk pangkat 3)
e. Rumus Luas Permukaan Kubus = 6 x rusuk x rusuk
f. Luas salah satu sisi = rusuk x rusuk
g. Keliling kubus = 12 x rusuk
h. Panjang diagonal bidang = rusuk x V2
i. Panjang diagonal ruang = rusuk x V3
 |
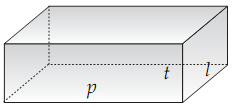
| Bangun Ruang Balok |
Ketentuan pada bangun ruang balok :
a. Terdapat 6 (enam) buah sisi yang berbentuk empat persegi panjang dengan luas yang sama
b. Terdapat 12 (dua belas) rusuk, masing-masing terdapat 4 (empat) rusuk dengan panjang yg sama.
c. Luas sisi balok yang berdapan adalah sama, dimana terbagi menjadi 3 bagian sisi yang saling berhadapan
d. Semua sudut pada balok adalah siku-siku
e. Rumus Volume Balok = p x l x t (sebenarnya sama dengan kubus, hanya saja kubus memiliki semua rusuk yang sama panjang).
f. Luas Permukaan Balok = 2 x {(pxl) + (pxt) + (lxt)}
g. Keliling Balok = 4 x (p + l + t)
h. Diagonal Ruang = Akar dari (p kuadrat + l kuadrat + t kuadrat)
 |
| Bangun Ruang Bola |
Ketentuan pada bangun ruang bola :
a. Pada bola terdapat jari-jari dengan panjang yang sama ke segala arah dari titik pusat bola
b. Garis yang membelah bola melewati titik pusat adalah garis tengah ( 2 x jari-jari)
c. Bola itu berbentuk bundar merata kesegala arah
d. Rumus Volume Bola = 4/3 x phi x jari-jari x jari-jari x jari-jari
e. Rumus Luas Bola = 4 x phi x jari-jari x jari-jari
f. Phi = 3,14 atau 22/7
 |
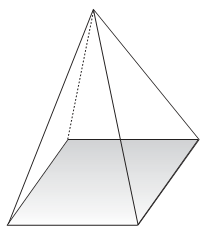
| Bangun Ruang Limas |
Ketentuan pada bangun ruang limas :
a. Bisa mempunyai bentuk alas yang berbeda-beda seperti segitiga, segi empat, segi lima dan lain-lain.
b. Rumus untuk mencari volume limas adalah 1/3 x luas alas x tinggi
c. Mencari luas alas bergantung pada bentuk alas
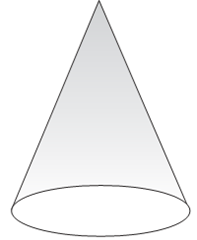
d. Biasanya alas bersifat segi sedangkan jika bundar disebut kerucut.
Itulah sekilas tentang rumus bangun ruang lengkap yang bisa saya hadirkan untuk anda. Jika anda merasa beberapa contoh di atas tidak lengkap, maka anda bisa mencari lagi di search engine internet. Menurut saya pribadi pada dasarny rumus volume pada setiap bangun ruang itu prinsipnya adalah sama yaitu perkalian sumbu x, y dan z. Tetapi ada penyesuaian rumus dikarenakan bentuknya yang beragam.
Bangun ruang disebut juga bangun tiga dimensi. Bangun ruang merupakan sebuah bangun yang memiliki ruang yang dibatasi oleh beberapa sisi. Jumlah dan model sisi yang membatasi bangun tersebut menentukan nama dan bentuk bangun tersebut. Misalnya:
| - | Bangun yang dibatasi oleh 6 sisi yang sama ukuran dan bentuknya, disebut bangun kubus. |
| - | Bangun yang dibatasi oleh 6 sisi yang mempunyai ukuran panjang dan lebar (persegi panjang) disebut bangun balok dan prisma. |
| - | Bangun yang dibatasi oleh sisi lengkung dan dua buah lingkaran, disebut bangun tabung.
|
Jumlah serta model sisi yang dimiliki oleh sebuah bangun tertentu merupakan salah satu sifat bangun ruang tersebut. Jadi, sifat suatu bangun ruang ditentukan oleh jumlah sisi, model sisi, dan lain-lain.