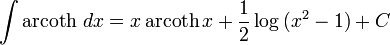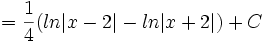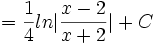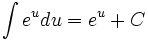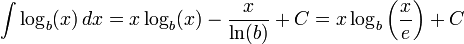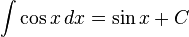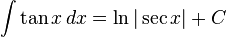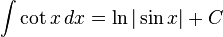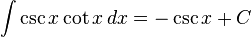Kamis, 30 Agustus 2012
Rabu, 08 Agustus 2012
Integral
Aturan integrasi dari fungsi-fungsi umum
Integral dari fungsi-fungsi sederhana
Fungsi rasional
Fungsi irrasional
Logaritma
Fungsi eksponensial
Fungsi trigonometri
- Artikel utama: Daftar integral dari fungsi trigonometri dan Daftar integral dari fungsi arc

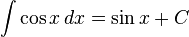














Fungsi hiperbolik
Fungsi inversi hiperbolik
Integral
Mencari nilai integral
Substitusi
- Contoh soal:
- Cari nilai dari:

Integrasi parsial
- Integral parsial menggunakan rumus sebagai berikut:
- Contoh soal:
- Cari nilai dari:


- Gunakan rumus di atas
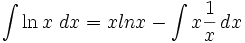


Substitusi trigonometri
| Bentuk | Gunakan |
 |
 |
 |
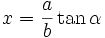 |
 |
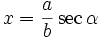 |
- Contoh soal:
- Cari nilai dari:

-
-
- Cari nilai dari:
 dengan menggunakan substitusi
dengan menggunakan substitusi 




- Cari nilai dari:
-
-
- Masukkan nilai tersebut:
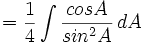


-
- Nilai sin A adalah


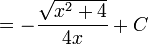
- Nilai sin A adalah
Integrasi pecahan parsial
- Contoh soal:
- Cari nilai dari:

- Akan diperoleh dua persamaan yaitu
 dan
dan 
- Dengan menyelesaikan kedua persamaan akan diperoleh hasil

Rumus integrasi dasar
Umum
Bilangan natural
Logaritma
Trigonometri
Pustaka : Wikipedia
Langganan:
Komentar (Atom)


![\int [f(x) + g(x)]\,dx = \int f(x)\,dx + \int g(x)\,dx](http://upload.wikimedia.org/wikipedia/id/math/e/7/d/e7d070d203baf49797b4e4a3fc3685f3.png)
![\int f(x)g(x)\,dx = f(x)\int g(x)\,dx - \int \left[f'(x) \left(\int g(x)\,dx\right)\right]\,dx](http://upload.wikimedia.org/wikipedia/id/math/3/b/8/3b8eab67c2a13a6392f41a8854cb2348.png)
![\int [f(x)]^n f'(x)\,dx = {[f(x)]^{n+1} \over n+1} + C \qquad\mbox{(untuk } n\neq -1\mbox{)}\,\!](http://upload.wikimedia.org/wikipedia/id/math/0/7/2/072d6a84d5c3d598b8f7a8aa86cb2f44.png)

![\int {f'(x) f(x)}\,dx= {1 \over 2} [ f(x) ]^2 + C](http://upload.wikimedia.org/wikipedia/id/math/0/c/6/0c64f04cc80db157abf9bbb321648b42.png)


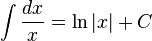
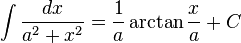





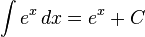






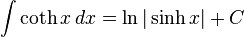
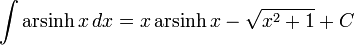


![\int \operatorname{arcsch}\,x \, dx = x \operatorname{arcsch} x+ \log{\left[x\left(\sqrt{1+\frac{1}{x^2}} + 1\right)\right]} + C](http://upload.wikimedia.org/wikipedia/id/math/1/0/f/10f33761c6822c44767d7aa10b2c71f1.png)